Simplify simply means to make it simple. In mathematics, simply or simplification is reducing the expression/fraction/problem in a simpler form. It makes the problem easy with calculations and solving. We can —
- simplify fractions by cancelling all the common factors from both the numerator and the denominator and writing the fraction in its lowest/simplest form.
- simplify mathematical expressions by grouping and combining similar terms. This makes the expression easily understandable and solvable.
How do you Simplify Step-by-Step?
Simplifying Fractions
Let’s understand the step by step procedure of simplifying fractions through some examples.
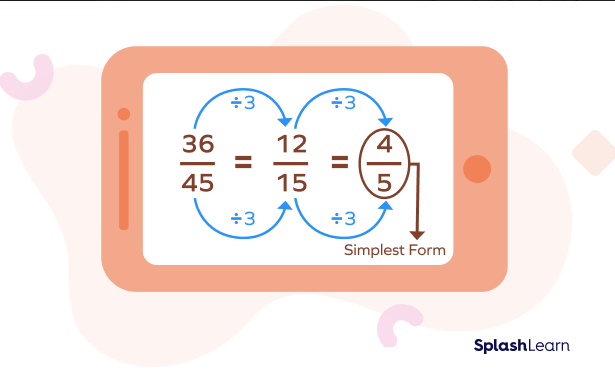

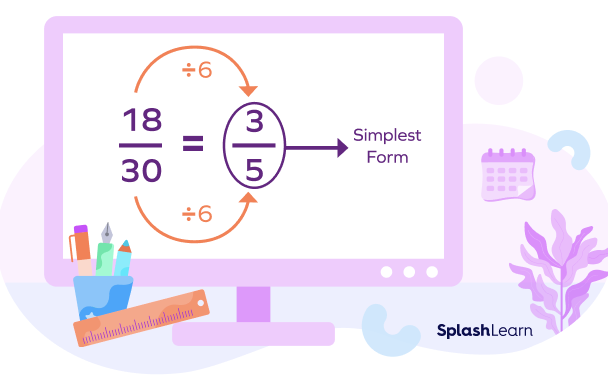
Do you know that instead of canceling out the common factors in multiple steps we can do it in single step as well. It gives the same simplest form of the fraction.
Simplifying Mathematical Expressions
Mathematical expressions are combination of various numbers and operations. So, to simplify them we need to know the rule known as the order of operations. It tells us the correct sequence in which the operations must be performed while simplifying a mathematical expression. We can remember the order using the acronym PEMDAS.

Recommended Games
Solved Examples:
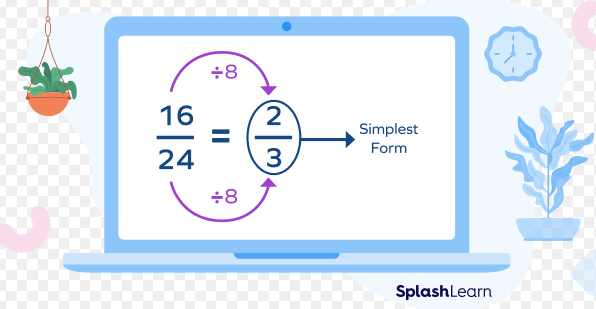
Example 1: Write 16/24 in the simplest form.
Example 2: Simplify: 110 – 35 × 2
Solution:
110 – 35 × 2 (As per PEMDAS, multiplication to be performed before subtraction)
= 110 – 70
= 30
Example 3: Simplify: 660 ÷ 22 × (2 + 1)
Solution:
660 ÷ 22 × (2 + 1) (Solve parenthesis first)
= 660 ÷ 22 × 3 (From left to right, division appears first)
= 30 × 3
= 90
Example 4: Simplify: 37 − [28 + (19 − 7)]
Solution:
37 − [28 + (19 − 7)] First solve ( )
= 37 − [28 + 12] Next, solve [ ]
= 37 − 40
= 77
Example 5: Simplify $1\frac{4}{7}\times 2\frac{4}{33} \div \frac{5}{9}$
Solution:
Simplyfly $1\frac{4}{7}\times 2\frac{4}{33} \div \frac{5}{9}$ Convert mixed fraction to improper fraction
= $\frac{11}{7}\times \frac{70}{33} \div \frac{5}{9}$
= $\frac{11}{7}\times \frac{70}{33} \div \frac{9}{5}$ Cancel the common factors
= $\frac{1}{1}\times \frac{2}{1} \div \frac{3}{1}$
= 6
Recommended Worksheets
Practice Problems
Simplify
Simplify the expression: 15 + 10 ÷ 5 = ?
Applying PEMDAS rule: 15 + 10 ÷ 5 = 15 + 2 = 17
Simplify the expression: 4 + (3 x 4) ÷ 22
Applying PEMDAS rule: 4 + (3 x 4) ÷ 22 = 4 + 12 ÷ 4 = 4 + 3 = 7
What is the simplest form of the fraction $\frac{12}{36}$ ?
Cancelling out the common factors we get $\frac{1}{3}$
Simplify the expression: $18 – [6 – {4 – (8 – 6 + 3 )}]$
$18 – [6 – {4 – (8 – 6 + 3 )}] = 18 – [6 – {4 – 5}] = 18 – [6 – {– 1}] = 18 – [6 + 1] = 18 – 7 = 11$
Frequently Asked Questions
What is simplification?
Simplification is the process of replacing a mathematical expression by an equivalent one, that is simpler, usually shorter.
How do you simplify mathematical expressions?
Order of operations play a major role in simplifying mathematical operations. The correct order of operations is: terms in parentheses, exponents, multiplication, division, addition, and, finally, subtraction. A handy acronym you can use to remember this is PEMDAS.
How do you simplify fractions?
A fraction is said to be in its simplest form if 1 is the only common factor of its numerator and denominator. Thus, to simplify a fraction, divide the numerator and the denominator by it’s highest common factor.
These were the basic rules and benefits of simplification in math. Every child should learn the concept as it makes solving complex problems relatively easy. If you are looking for a platform to teach your child mathematics through fun games, try SplashLearn by signing up for free. Since math can be daunting for some children, fun games and puzzles make it seem interesting and much more comprehensive! To know more about the concepts of simplification and other math topics, visit us at: https://www.splashlearn.com/.




































